不同学科之间之所以能够相互借鉴、触类旁通,根本原因在于它们在深层次上拥有相似的抽象结构。当变化未触及这一抽象本质时,可类比为拓扑学中的同伦变换——结构保持一致,只是形式发生了变化。而一旦变化触及抽象本质,我们则称之为“蜕变”或“范式转变”。在许多情况下,这种抽象本质可以用数学模型来表达。以扩散模型为例,它不仅仅是气体密度的变化,也是绘画中的点彩技法,或者近年来获得极大进步的“根据文字智能生成图片”技术。是抽象结构跨领域运用的生动体现。
什么是扩散模型
要了解扩散模型的精髓,需要从物理中实际存在的扩散现象说起。在气体中,分子会由高浓度区向低浓度区扩散,逐渐扩散成一致的分布。这种过程,可以用扩散方程或更一般的 Fokker-Planck 方程来建模,是概率论与物理实验的基石。
扩散模型就是模仿了这种现象,将真实的数据(比如一幅图片),逐渐加入随机噪声,直到全部变成纯粹的高斯白噪声。但真正的灵魂,在于反向过程:从纯随机噪声出发,经过一段段小步骤的去噪,最终还原成有结构、有细节的数据。这个去噪过程,有目的,有提示,但是每一次可以使用随机的种子,因此可以生成多种多样,且符合要求的画面数据。
在扩散模型中,正向扩散阶段故意加入大量随机噪声,让数据逐步模糊甚至看似消失。而在逆向去噪过程中,神经网络引导生成系统一点一点去除噪声,逐步恢复隐藏在噪声背后的抽象结构。
噪声本身不含有任何有用的数据,但是扩散模型的神经网络在训练过程中学到了一套”去噪流程”,这是一个函数族,近似于物理反扩散的逆过程。模型的训练目的是回答这个问题:“从稍微干净一点的噪声,最可能变成什么真实数据”。神经网络不是从白噪声中发现模式,而是从白噪声出发,根据去噪步骤一步步制造模式!所以白噪声只是一个初始原料,真正决定模式的是神经网络。
数学上,扩散模型是在做有条件的采样,给一团噪声,不是瞎猜,而是根据模型学习到的概率规则,指导我们一步步往目标数据分布靠近。白噪声包含随机性也非常重要,它可以让模型生成多样化、丰富的结果。如果用全零作为起点,只能得到单一、僵化的结果。
为什么扩散模型有效?
在人类认知中,识别事物往往并不依赖于表面细节的完美一致,而是依赖于一种更深层的抽象结构。
比如,一只猫的图像,即使加上一些噪声、改变角度、拉伸比例,我们通常仍然能够毫无困难地认出那是一只猫。
这是因为,人类识别的是猫的本质特征,而不是表层像素的排列。
这些“扰动”——噪声的加入、角度的变化、形状的轻微扭曲——从拓扑学角度看,就是同伦变换:一种在连续变形中保持本质结构不变的变换。
同伦变换的思想告诉我们:
- 如果两个对象之间可以通过连续变化互相变换,并且在变化过程中没有撕裂或粘连,那么它们可以被看作本质上是同一种结构。
- 加噪声、换角度、局部拉伸这些操作,并没有破坏“猫”的基本拓扑特征,因此在我们心目中,它仍然是“同一只猫”。
正是因为猫的“同伦不变性”——即便被噪声扰动,其本质特征仍然存在——扩散模型才能成功地从纯噪声中,重构出一只自然、可信的猫。
换句话说,扩散模型的成功正是因为世界的抽象结构在小幅扰动下是稳定的,而神经网络学会了如何沿着这些稳定的同伦轨迹去寻找、复原真实世界的数据分布。
扩散模型之所以有效,不是因为噪声本身包含了信息,而是因为神经网络在每一步去噪时,把训练期间学到的规律添加到生成过程中,逐渐从随机形态构建起有结构的结果。
与其它数学模型的联系
扩散模型和隐马尔可夫过程(HMM)有相似性,它们都从可以观测值去推理出实际值。然而,它们的数学原理、应用领域以及生成目标存在明显的差异。隐马尔可夫过程通常用于推断隐状态,而扩散模型则用于生成数据,尤其适用于图像生成、语音合成等任务。
HMM是一种基于状态转移模型的概率图模型,它假设系统的状态在时间上遵循马尔可夫假设,即当前状态只依赖于前一个状态。在HMM中,状态是隐含的,而观测值是通过状态生成的,通常通过贝叶斯法则和最大似然估计MLE来估计模型参数。主要用途包括语音识别、手写识别。其中隐状态是系统的内部状态,如语音的声学状态。
相比HMM,扩散模型是一种基于随机过程的生成模型,特别是在图像生成和声音合成中应用较多。它通过在正向扩散过程中逐步添加噪声,直到数据变成纯噪声,然后在反向扩散过程中恢复出原始数据。它的模型需要利用变分推断和神经网络来训练,生成数据的过程通常通过优化损失函数来实现。它的目标是生成数据,而不是推断状态。
虽然看上去很不同,但是扩散模型和布朗运动模型有很多联系,因为它们都涉及到随机扰动和逐步演变。布朗运动被建模为一个连续时间、连续空间的随机过程,通常使用Wiener过程,以随机微分方程来表示。它主要用来建模描述随机世界。扩散模型的正向过程和布朗运动有类似的随机性,其方程基本一致。而扩散模型的反向过程则是真正的有价值之处,生成数据。
扩散模型的用途
除了图像之外,扩散模型还用于语音、音乐等多个领域。
在图像生成领域,扩散模型和传统生成模型GAN有着显著的区别。GAN 模型需要通过两个模型(生成器和分辨器)的博弈,带来了训练不稳定和模式崩坏等问题;而扩散模型,减缓了生成过程的复杂度,用深度神经网络学习从随机到有结构的过程,训练稳定,生成效果出色。
这种方式,不仅在图像上大放光芒,在语音和音乐领域同样得到了辉煌的成绩。语音是连续信号,比起文本这种离散类数据,更适合扩散转换。像 Grad-TTS 这样的系统,用扩散模型从文本直接生成声谱,再转化为声波,进一步提升了自然度和细节感。在音乐领域,扩散模型展示了发挥创造力的突破性。Dance Diffusion 等项目,使用扩散生成音段,在持续性与多样性之间找到了完美的平衡。AudioLDM 等新技术,以文本为条件,生成环境音和纯音乐,进一步拆除了类别间的隔阅。但是扩散模型用于文本生成还是存在很大的挑战。因为文本生成具有的离散性,难以用扩散模型实现。
与绘画艺术的联系
噪声是空白的画布,而扩散模型,则是点彩技法(Pointillism),它细细地绘出有生命力的作品。“大碗岛的周日午后”这幅画是点彩技法的巅峰之作。画家乔治·修拉(Georges Pierre Seurat)耗时两年半,点了数十万个色彩小点,组成了一幅宏大而生动的画作,仔细看每一个点,好像都是随机的无序,但是它们逐步累积起来,展现了一个美丽和复杂的世界,最终形成一幅清晰、富有表现力的整体。这是一个从无到有、从模糊到清晰的渐进式艺术创作。2024年的芝加哥之行,我有幸瞻仰这幅画的原作,令人惊叹不已。
扩散模型是一种新的计算模式:它不再是分布式多维数据结构的降维打击,而是逐步改进,调和随机与规律,从随机的空白中生出万物。人类识别世界,是识别同伦不变的抽象结构;扩散模型复原数据,也是沿着同伦轨迹重建秩序。
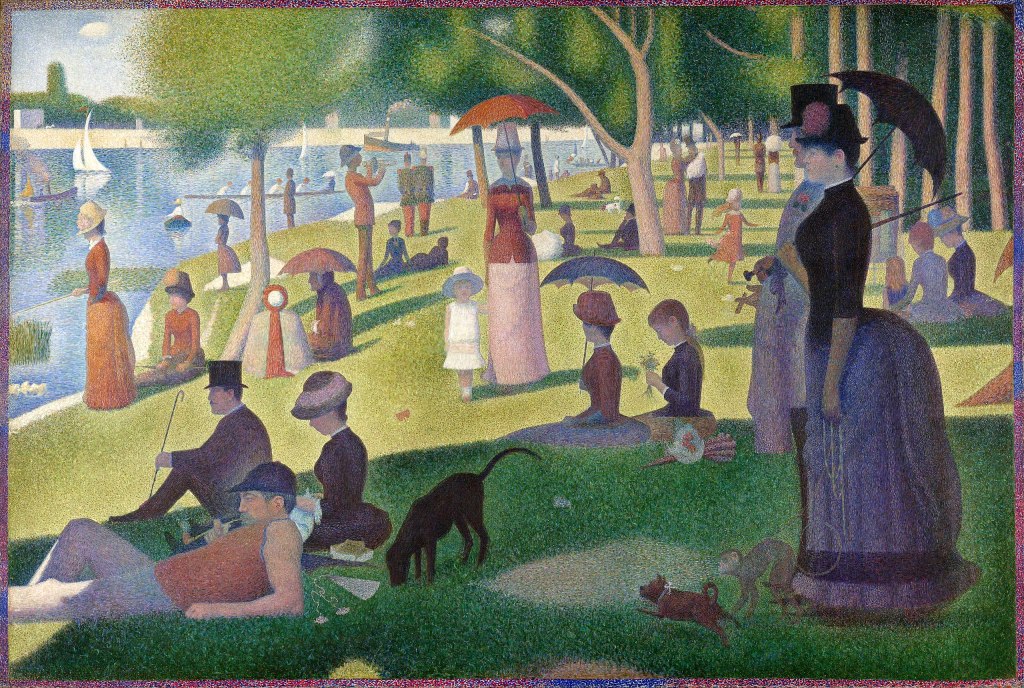
发表评论