高维度词嵌入的相对位置不变性

当前自然语言处理中广泛使用的自注意力（Self Attention）是一种高度并发的软键值查询，它返回加权运算后的概率值。而用于其输入的词语向量（Word Embedding）本身不携带任何位置信息。因此如果一句话的词语序列发生变化，在运算后会产生一模一样的最终值，导致模型不能理解“我爱你”和“你爱我”之间的语义区别。

为了区分语序的不同带来的不同语义，在从2017年以来的一系列论文里，研究人员提出了各种位置编码，它与词语向量一起作为模型的输入来产生不同的语义结果。其发展历程涵盖了：绝对位置编码，神经网络学习的编码，偏置编码等等。

自然语言具有一些特性，比如在句子首部中插入一两个词不改变意义。比如这两个句子：“我爱你”，“所以我爱你”。在这两个句子中，“我爱你”这个部分的语义相同，虽然“我”这个词在句子中的绝对位置从1变化为3，“你”这个词在句子中的绝对位置从3，变化为5，但是“我爱你”这个短语的相对位置没有发生变化，“你”仍然在“我”之后两个位置，其语义的数学表达也应该保持不变。

总而言之，一个好的位置编码计算出的向量之间的内积应该只依赖于它们的相对位置，这样可以让模型学到文本的平移不变性（Translation Invariance），即相同排列的词语之间的关系不会因为在句子中的绝对位置不同而改变。几何学上，物体仅仅是坐标变化了，其本质并无改变。这是一种基础的对称性，女科学家Emma Noether 用它推导出动量守恒原理。因此坐标的绝对值不应参与计算，仅仅用坐标相对值进行计算。其数学公式如下：

满足这个公式就意味着注意力计算仅依赖于相对位置  i – j ，而不是绝对位置  i, j  本身。而向量的内积与其夹角的余弦成正比，因此向量夹角是一个很合适的表达向量之间相对位置的数值。

Transformer发布的时候采用了正余弦位置编码，仍然是绝对位置编码，本质上是傅立叶变换。现代的大语言模型经常运用RoPE（旋转位置编码，Rotary Position Embedding）来表明词语之间的相对位置，RoPE是一种只关注相对位置的编码方式。两个向量在同时旋转的时候其夹角保持不变。在数学上，旋转是一个正交变换（Orthogonal Transformation），既不改变向量的内积（词语之间的距离），也不改变其范数（词语的相对重要性），因此，把向量之间的夹角当作它们之间的距离会非常方便，是一种特别合适编码词语位置的数学工具。

下面是一个二维旋转矩阵，其中 theta 是旋转角度。这样，在计算词语之间的内积的时候，仅仅考虑其相对位置，而其绝对位置对最终结果并无影响。

但是语言本身具有非常多的维度，从数百维到数万维不等，在  d  维空间中，完整的旋转矩阵是一个  d x d  的矩阵，它和它的转置矩阵相乘会得到单位矩阵。其行列式的值为1。

一个完整的  dxd  旋转矩阵需要存储  d^2  个参数，并且矩阵乘法的计算复杂度为  O(d^2) 。

当 维度  d  很大时（如 768 维的 BERT 或 12288 维的 GPT-3），这种计算开销非常昂贵。

但实际上，所有的旋转矩阵都必须正交，因此它们的自由度只有  d(d-1)/2 ，如果没有自由度的约束，矩阵运算会需要很多参数。在高维度的时候，自由度通常远远小于  d^2 ，这意味着我们可以使用 多个 2D 旋转块 进行计算，而不需要完整矩阵。

比如：在 2D 空间（ d = 2 ）：只有 1 个旋转自由度（旋转角度  theta ）。

在 3D 空间（ d = 3 ）：有 3 个旋转自由度（绕  x, y, z  轴的旋转角度）。

在 4D 空间（ d = 4 ）：有 6 个旋转自由度（六个独立的 2D 旋转平面）。

在高维空间中，旋转不是一个单一的操作，而是多个 二维平面上的旋转组合，例如：

在 3D 中，旋转可以分解成绕  xy 、 yz  和  xz  平面的三个旋转。

在 4D 中，我们有 6 个旋转自由度，对应于 6 个不同的 2D 旋转平面。

因此，我们采用 多个独立的 2D 旋转块来实现高维旋转，就可以避免存储 d^2个参数，以及 O(d^2)的计算复杂度。这种数学运算称作 Givens 旋转（Givens Rotation）

对于  d  维向量，每两维作为一组，进行 2D 旋转，就可以保持其相对位置不变。例如，在 4D 情况下，我们有：

第一对 (x_1, x_2) 进行旋转角度  theta_1 

第二对 (x_3, x_4) 进行旋转角度  theta_2 

旋转角度  theta  可以随着维度的增加而变化，以提供不同层级的位置信息。四维空间里面的旋转矩阵如下：

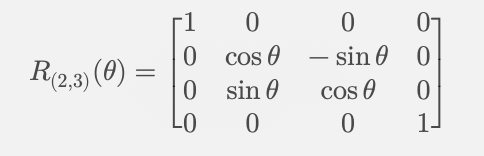
通过将高维度向量拆分成多个 2D 子空间进行旋转，RoPE 可以在所有维度中自然地编码位置信息，而不需要额外的训练参数。

RoPE（旋转位置编码，Rotary Position Embedding） 的核心思想：

直接作用在 Query 和 Key 上，而不是 Value

使用旋转矩阵（Rotation Matrix）编码相对位置信息，使注意力计算只依赖于相对位置信息  i – j

计算过程仍然是内积计算（Dot Product），但内积值仅依赖于相对位置。

目前大量的论文集中在如何优化Self Attention机制上，位置编码也是热点之一。

数学的抽象性使其能够跨越具体应用，在不同领域找到意想不到的用途。线性代数中的旋转矩阵，最初在物理学、计算机图形学、机器人学等领域中用于描述刚体变换。现在也被应用于自然语言处理（NLP）和深度学习，特别是在相对位置编码和Transformer 结构优化等方向。

旋转矩阵、高维对称性、群论、以及拓扑数学在凝聚态物理（Condensed Matter Physics），尤其是晶格结构、能带理论和拓扑物理中起到了核心作用。许多在机器学习（如 Transformer 和 RoPE）中使用的数学工具，在物理学中早已被深入研究，并且启发了 AI 领域的一些关键技术。

NLP 领域仍然有许多挑战，包括：

✅ 计算效率 & 长序列建模（如降低 Transformer 计算复杂度）

✅ 位置编码 & 结构化建模（如更好地处理长文本、跨语言翻译）

✅ 推理能力 & 知识建模（如让大模型真正 “思考” 而不仅是模式匹配）

✅ 跨语言公平性（如让所有语言都得到良好的 NLP 支持）

✅ 安全性 & 对抗性训练（如让 AI 更安全可靠）

✅ 低资源微调（如让小公司也能训练 LLM）

未来几年，预计模块化 AI、混合建模（Neuro-Symbolic AI）、更高效的 Transformer 替代架构（如 Mamba）会成为热门研究方向

未来的大模型研究，很可能会在更深入的数学抽象中找到新的突破点！